Daily Archives: 24/07/2023

Investigating Trigonometric Ratios

This classroom activity uses the Geogebra tool to derive and explore the trigonometric ratios. A right-angled triangle with given angles is created precisely and enlargements of this triangle are created. Ratios between sides are calculated and compared across all the triangles. These ratios are then compared with the sine, cosine and tangent trigonometric ratios for the given angles.

In this investigation you will explore similar right-angled triangles. Each student will explore a triangle with different angles.

  1. Record the angle assigned by your teacher, or randomly select an
    angle between 30∘ and 75∘.
  2. Open a new Geogebra window, ensuring that the grid and axes are
    both showing.

Create a right-angled triangle, with one of the angles matching your
assigned angle, using the following steps:

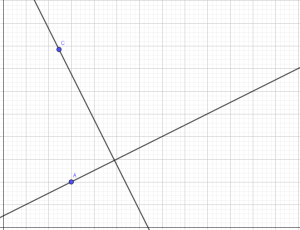
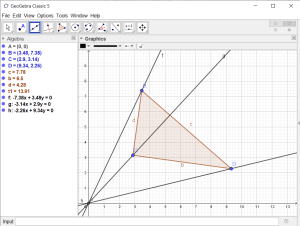
  1. Create a line using the “Line” tool and a second perpendicular
    line using the “Perpendicular Line” tool. The intersection of these two
    lines will form the right-angle of our right-angled triangle.

  2. Create an angle with the size specified in (1) using the “Angle
    with Given Size” tool

    1. Create a point D on the first line using the “Point on Object”
      tool. The point should appear to the right of the intersection between
      the two lines as shown in the diagram below.
    2. Select the “Angle with Given Size” tool
    3. Click on point A
    4. Click on point D
    5. Select clockwise for the angle measure
    6. Enter the size of the angle (as given in (1))
    7. Use the “Line” tool to connect the two newly created points
      (points A’ and D in the diagram below).

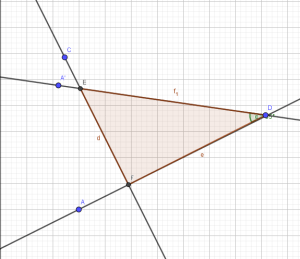
  3. Create two additional points (E and F below) at the intersections
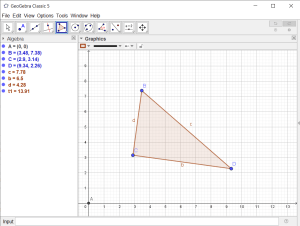
    of the lines using the “Intersect” tool.
  4. Form a triangle using the “Polygon” tool that connects the three
    intersection points.

  5. Use the “Angle” tool to show the three angles within the
    triangle.
  6. Hide the unnecessary lines and points used in creating the
    triangle by de-selecting the objects in the Algebra View.

  7. Measure the lengths of each side in the triangle.
  8. Save your file at this stage (if not done so already) and export
    an PNG image file of your right-angled triangle.
  9. Using the enlargement transformation method used in Part 1,
    create enlargements of your right-angled triangle with scale factors of
    2 and 4.
  10. Measure all sides and angles in the two enlargements. Save your
    file and export a PNG image file.
  11. Record all angles, side lengths and side ratios in a table like
    the following. You should record the lengths to 5 decimal places. Go to
    Rounding under the Options menu and change the rounding settings.

    Angle Opp Adj Hyp \dfrac{Opp}{Adj} \dfrac{Opp}{Hyp} \dfrac{Adj}{Hyp}
    Triangle 1
    Triangle 2
    Triangle 3

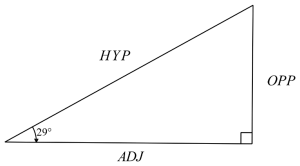
The angle is the one given in (1). Opposite, adjacent and hypotenuse
are all measured from the given angle as shown in the following
diagram.

  1. Comment on the ratios between the three sides for the three
    triangles as shown in the table created in step (13).
  2. For your given angle, use your calculator to complete the
    following table.

    tan  θ sin  θ cos  θ
    θ=  
  3. Using the tables from (13) and (15) complete the following rules

    \tan \theta =

    \sin \theta =

    \cos \theta =

  4. Repeat step (13) using the other acute angle in your triangle,
    recording your measurements and calculations in a new table.
  5. Using the tables from (13), (15) and (17) define a rule(s) that
    connects the sine and cosine functions.

Investigating similar triangles using Geogebra

To explore properties of similar triangles we will apply enlargement transformations to a triangle using the Geogebra tool.


You can either use the online version of Geogebra or you can download Geogebra Classic 5 or Geogebra Classic 6. Note that the screen shots shown below are based on Geogebra Classic 5, however Geogebra Classic 6 is very similar.

  1. Open a new Geogebra window, ensuring that the grid and axes are shown.

  2. Using the “Move Graphics View” tool, move the window so that the window is focussed on the 1st quadrant of the Cartesian plane.

  3. Use the “Point” tool to create a point at the origin of the Cartesian plane (0,0). This is referred to as the enlargement origin.

  4. Use the “Polygon” tool to create a triangle with all three vertices in the 1st quadrant.

  5. Use the “Line” tool to create three lines that each pass through the transformation origin and one of the vertices of the triangle.

  6. Use the “Enlarge from Point” tool to create a second triangle which is an enlargement of the first.
    1. Select the “Enlarge from Point” tool

    2. Click on the original triangle
    3. Select the enlargement origin
    4. Enter a scale factor of 2

  7. Measure the three internal angles of the first triangle

    1. Select the “Angle” tool

    2. Click within the first triangle – all three angles should be
      marked.

  8. Repeat the above steps to measure all three internal angles of
    the second triangle.

  9. Record your measurements in a table like the one below:

    Angle 1 Angle 2 Angle 3
    Triangle 1
    Triangle 2

  10. Measure the three sides of the first triangle

    1. Select the “Distance or Length” tool

    2. Select the two vertices at either end of the side

    3. Repeat for the other two sides

  11. Repeat the above steps for the second triangle.

  12. Record your measurements in a table like the one below. Include
    calculations of the ratios between side lengths for each of the two
    triangles.

    Side 1 Side 2 Side 3 Side 1 ÷
    Side 2    		 Side 1 ÷
    Side 3    		 Side 2 ÷
    Side 3
    Triangle 1
    Triangle 2

  13. Calculate the area of the first triangle using the “Area” tool

    1. Select the “Area” tool

    2. Click on the triangle

  14. Repeat for the second triangle.

  15. Insert your measurements of area in a table like the one
    below:

    Area
    Triangle 1
    Triangle 2

  16. Save your Geogebra file as “enlargement_transformation.ggb” using
    “Save” from the “File” menu.

  17. Export your enlargement diagram to a “PNG” file using
    “Export”->”Graphics View” from the “File” menu.

  18. With reference to your measurements in the three tables, comment
    on how the angles, side lengths, rations between sides, and area are
    affected by an enlargement transformation with a scale factor of
    2.

  19. Predict what will happen to the angles, side lengths, ratios
    between sides, and area, if the original triangle is enlarged by a scale
    factor of 3.

  20. Use Geogebra to test your prediction, include an exported image
    file as evidence.

  21. Summarise your findings with four hypotheses relating to the
    angles, side lengths, ratios between sides, and area of enlarged
    triangles with a scale factor of n.