Asteroids Simulator

Aug2

This article explains how to develop a simulator of part of an Asteroids game in Geogebra using parametric curves based on position vectors. Note that this simulator is intended for exploring mathematical models and as such many of the details of a full Asteroids game have been abstracted.

The animated gif image below is an example of a simple simulator developed in Geogebra. The large circle represents an Asteroid, while the smaller circle (dot) represents a missile that has been fired. The simulator demonstrates whether or not the missile hits the Asteroid and can be used to determine the minimum distance between the centre of the Asteroid and the missile.

Before we create the simulator, we provide a brief description of the main components of the Geogebra tool.
The screenshot below shows Geogebra Classic 6. On the left-hand side is the Algebra window. This is where we will input components of the mathematical model, including curves and points. The middle and main part of the display is the Graphic window, this is where the asteroids model will be displayed. The toolbar at the top of the screen provide access to the main geometric tools – in this article we some of these tools to create a slider, create a circle to represent an asteroid and add text showing the distance between two points.

The highlighted settings button allows for the configuration of elements on the Graph window. Clicking on the background allows us to configure the background window.

Step 1: Screen dimensions

We begin by setting the screen dimensions. We assume that the game is played on a 4:3 aspect ratio with a resolution of 800 pixels wide and 600 pixels high. In Geogebra we will let 1 unit represent 1 pixel in the game. As such the range of x values will be between 0 and 800, while the range of y values will be between 0 and 600. Settings for this in Geogebra are shown below. Note that maximum x and y values go slightly beyond the range. Note also that we have a 1:1 ratio between the x and y scales. To access the configuration options for the background, click on the settings button.

Step 2: Representing time

Time (in seconds) will be represented using a slider. For our example time will range from 0 to 10 seconds, with increments of 0.01 seconds. This slider is created using the slider tool.

The configuration options are shown in the following image.

The width of the slider is increased from the default of 200 pixels to 500 pixels. To configure this right-click on the slider and select “Settings”.

The settings window for the slider is shown below with the updated width value highlighted.

Step 3: Modelling a missile

The missile in our example has an initial position of (30, 40) and a velocity vector of [50, 30]. The position vector (relative to the origin) is given as follows.
$\vec{r_A} = [30, 40]+t[50,30]$
To represent this position vector in Geogebra we use the Curve function. The function takes parameterised expressions for the x-coordinates and y-coordinates of points on the curve, together with parameter used in the expressions, and the lower and upper limits of values passed to the parameter. In this case we use the variable t as the parameter and set the range of values from 0 to 10. The input for this in Geogebra is as follows:

Curve(30+50t, 40+30t, t, 0, 10)

To trace the path of the missile at a particular time we create a new point representing the point on the curve for the current value of the time variable. The input for this in Geogebra is given below:

a(t)

The details of the curve and parameterised point should appear in Geogebra as shown in the screenshot below.

The graphing window should look like the screenshot below after the commands shown above have been entered. It shows the path that the missile will take over the 10 second time interval, together with the current position of the missile (shown as point A). The time variable has a value of 0 and the missile is at its starting position of (30, 40).

Step 4: Modelling an asteroid

Next we model an asteroid with an initial position of (400, 250) and a velocity vector of [-20, -30]. The asteroid will be modelled as a circle with a diameter of 80 pixels. The position vector (relative to the origin) of the asteroid is given as follows.
$\vec{r_A} = [400, 250]+t[-20,-30]$
The path of the asteroid is modelled using the Curve function in Geogebra.

Curve(400-20t, 250-30t, t, 0, 10)

Next, the centre of the asteroid is modelled as a parameterised point.

b(t)

Finally, a circle whose centre is the parameterised point is created using the “Circle: Center and Radius” tool.

The radius of the circle is 40 pixels. The details of the curve, parameterised point and circle are shown in the screenshot below.

After these commands have been added the graphing window should look like the screenshot below.

Step 5: Tracking the distance between objects

To determine whether the missile hits the asteroid we will track the distance between the centres of these objects. We begin by choosing the “Distance or Length” tool and selecting the point representing the missile and the point representing the centre of the asteroid (points A and B). This will create a distance calculation object together with a text object to display the distance.

Double-clicking on the text element pops up a window allowing us to edit the text. In this case we change the text on the left-hand side of the equal sign as shown in the screenshot below.

We then open the settings for the text object and click on the Pin to Screen option. Selecting this lets us move the text to the top of the screen.

After these steps have been completed the Graphic Window will look like the screenshot below (note this also includes a change in colour for the asteroid which is accessed by clicking on the asteroid object and then selecting settings).

Extra bling

The look of the simulator can be improved by adding a space background. This is done by choosing the “Image” tool.

In this case an image that has the correct 4:3 aspect ratio is chosen. The image appears in the middle of the Graph window as shown in the following screenshot.

The anchor points of the image (points C and D) are so that the image covers an 800×600 area.

The final result is shown in the following screenshot.

Investigating Trigonometric Ratios

Jul24

This classroom activity uses the Geogebra tool to derive and explore the trigonometric ratios. A right-angled triangle with given angles is created precisely and enlargements of this triangle are created. Ratios between sides are calculated and compared across all the triangles. These ratios are then compared with the sine, cosine and tangent trigonometric ratios for the given angles.

In this investigation you will explore similar right-angled triangles. Each student will explore a triangle with different angles.

Record the angle assigned by your teacher, or randomly select an
angle between 30^∘ and 75^∘.
Open a new Geogebra window, ensuring that the grid and axes are
both showing.

Create a right-angled triangle, with one of the angles matching your
assigned angle, using the following steps:

Create a line using the “Line” tool and a second perpendicular
line using the “Perpendicular Line” tool. The intersection of these two
lines will form the right-angle of our right-angled triangle.
Create an angle with the size specified in (1) using the “Angle
with Given Size” tool
1. Create a point D on the first line using the “Point on Object”
  tool. The point should appear to the right of the intersection between
  the two lines as shown in the diagram below.
2. Select the “Angle with Given Size” tool
3. Click on point A
4. Click on point D
5. Select clockwise for the angle measure
6. Enter the size of the angle (as given in (1))
7. Use the “Line” tool to connect the two newly created points
  (points A’ and D in the diagram below).
Create two additional points (E and F below) at the intersections
of the lines using the “Intersect” tool.
Form a triangle using the “Polygon” tool that connects the three
intersection points.
Use the “Angle” tool to show the three angles within the
triangle.
Hide the unnecessary lines and points used in creating the
triangle by de-selecting the objects in the Algebra View.
Measure the lengths of each side in the triangle.
Save your file at this stage (if not done so already) and export
an PNG image file of your right-angled triangle.
Using the enlargement transformation method used in Part 1,
create enlargements of your right-angled triangle with scale factors of
2 and 4.
Measure all sides and angles in the two enlargements. Save your
file and export a PNG image file.
Record all angles, side lengths and side ratios in a table like
the following. You should record the lengths to 5 decimal places. Go to
Rounding under the Options menu and change the rounding settings.

Angle Opp Adj Hyp $\dfrac{Opp}{Adj}$ $\dfrac{Opp}{Hyp}$ $\dfrac{Adj}{Hyp}$

Triangle 1

Triangle 2

Triangle 3

The angle is the one given in (1). Opposite, adjacent and hypotenuse
are all measured from the given angle as shown in the following
diagram.

Comment on the ratios between the three sides for the three
triangles as shown in the table created in step (13).
For your given angle, use your calculator to complete the
following table.

tan θ sin θ cos θ

θ=
Using the tables from (13) and (15) complete the following rules

$\tan \theta =$
$\sin \theta =$

$\cos \theta =$
Repeat step (13) using the other acute angle in your triangle,
recording your measurements and calculations in a new table.
Using the tables from (13), (15) and (17) define a rule(s) that
connects the sine and cosine functions.

	tan θ	sin θ	cos θ
θ=

Investigating similar triangles using Geogebra

Jul24

To explore properties of similar triangles we will apply enlargement transformations to a triangle using the Geogebra tool.

You can either use the online version of Geogebra or you can download Geogebra Classic 5 or Geogebra Classic 6. Note that the screen shots shown below are based on Geogebra Classic 5, however Geogebra Classic 6 is very similar.

Open a new Geogebra window, ensuring that the grid and axes are shown.
Using the “Move Graphics View” tool, move the window so that the window is focussed on the 1st quadrant of the Cartesian plane.
Use the “Point” tool to create a point at the origin of the Cartesian plane (0,0). This is referred to as the enlargement origin.
Use the “Polygon” tool to create a triangle with all three vertices in the 1st quadrant.
Use the “Line” tool to create three lines that each pass through the transformation origin and one of the vertices of the triangle.
Use the “Enlarge from Point” tool to create a second triangle which is an enlargement of the first.
1. Select the “Enlarge from Point” tool
2. Click on the original triangle
3. Select the enlargement origin
4. Enter a scale factor of 2
Measure the three internal angles of the first triangle
1. Select the “Angle” tool
2. Click within the first triangle – all three angles should be
  marked.
Repeat the above steps to measure all three internal angles of
the second triangle.
Record your measurements in a table like the one below:

Angle 1 Angle 2 Angle 3

Triangle 1

Triangle 2
Measure the three sides of the first triangle
1. Select the “Distance or Length” tool
2. Select the two vertices at either end of the side
3. Repeat for the other two sides
Repeat the above steps for the second triangle.
Record your measurements in a table like the one below. Include
calculations of the ratios between side lengths for each of the two
triangles.

Side 1 Side 2 Side 3 Side 1 ÷
Side 2 Side 1 ÷
Side 3 Side 2 ÷
Side 3

Triangle 1

Triangle 2
Calculate the area of the first triangle using the “Area” tool

Select the “Area” tool
Click on the triangle

Repeat for the second triangle.
Insert your measurements of area in a table like the one
below:

Area

Triangle 1

Triangle 2
Save your Geogebra file as “enlargement_transformation.ggb” using
“Save” from the “File” menu.
Export your enlargement diagram to a “PNG” file using
“Export”->”Graphics View” from the “File” menu.
With reference to your measurements in the three tables, comment
on how the angles, side lengths, rations between sides, and area are
affected by an enlargement transformation with a scale factor of
2.
Predict what will happen to the angles, side lengths, ratios
between sides, and area, if the original triangle is enlarged by a scale
factor of 3.
Use Geogebra to test your prediction, include an exported image
file as evidence.
Summarise your findings with four hypotheses relating to the
angles, side lengths, ratios between sides, and area of enlarged
triangles with a scale factor of n.

	Area
Triangle 1
Triangle 2

Measurement Toolkit (part 3)

Jun5

Surface area calculator

In this tutorial we describe how to add functionality for calculating the surface area of various shapes to the Measurement Toolkit. The screenshot below shows the tool being used to calculate the surface area of a rectangular prism.

Surface Area Calculator

The tool is designed so that we can easily extend it with functionality for calculating the surface area for additional 3d shapes. The main steps involved in adding a new shape to the surface area calculator are:

Research the shape to determine an appropriate formula for calculating its surface area
Design and implement test cases that will be run to check the correctness of calculations in the tool
Code a function to calculate the surface area of the chosen shape
Create an image file to represent the shape in the tool
Link the calculation function and image to the main interface

In the following sections we will look at the process used to add cubes to the surface area calculator.
Given a cube with sides of length a, then the surface area is given by the following formula:
$SA=6a^2$
The formula is derived by noting that the cube has six faces of equal size. Each face is a square with dimensions of a by a units.

Designing test cases

The next step is design and implement test cases for calculating the surface area of a cube. These should be designed initially on paper before being added to surface area tester file.
For the first test case we consider a cube with sides of length 5 units:

$SA=6\times 5^2=6 \times 25 = 150\mathrm{units^2}$

For the second test case a side length of 3.275 units is selected. The resulting surface area is rounded to two decimal places:

$SA=6\times 3.275^2 = 64.35375 \approx 64.35 \mathrm{units^2}$

These test cases were then coded in the surface_area_tester.py file as shown below. The tester file imports the surface area file on line 2, which contains the surface area calculation functions. It is assumed that the function for calculating the surface area of a cube is called calc_cube_sa, which takes a single input representing the length of the cube edges. Because the expected answer for the second test case was rounded to 2 decimal places we use assertAlmostEqual which in this case checks that the value returned by the calc_cube_sa after rounding to 2 decimal places is equal to the expected answer of 64.35.

import unittest
from surface_area import *

class TestSurfaceArea(unittest.TestCase):
    def test_calc_cube_sa(self):
        self.assertEqual(calc_cube_sa(5),150)
        self.assertAlmostEqual(calc_cube_sa(3.275),64.35,2)

if __name__ == '__main__':
    unittest.main()

Note that in the code above we have placed two test cases within the same test function allowing us to group the tests together based on the shape being tested.

Coding the surface area calculation functions

Functions for calculating the surface area of different 3d shapes are include in the surface_area.py file. The following code listing shows the code for the calc_cube_sa function. The file also includes a code stub for calc_rprism_sa, which will be used to calculate the surface area of a rectangular prism.
The file imports the math package which will be used later for doing calculations involving the constant pi.

import math

def calc_cube_sa(length):
    return 6*(length)**2

def calc_rprism_sa(length,width,height):
    return 0

Functions for additional surface area calculations should be added after the given functions.

After the functions have been written they should be tested by running the test cases in surface_area_tester.py.

Creating 3d shapes

Images representing the different 3d shapes used in the surface area calculator tool need to be created and added to the Images directory.
The following link explains how to
create 3d shapes in Illustrator. Another option is to create the 3d shapes using Efofex Draw.

Linking the components in the main interface

The final step in creating and adding to the surface area functionality of the Measurement Toolkit is to incorporate the calculation functions and images in the main mathtoolkit.py file.

##
## ADD NEW SHAPES HERE FOR SURFACE AREA
##
sa_shapes['Cube']=[['l'],"Images/cube.png","calc_cube_sa"]
sa_shapes['Rectangular Prism']=[['l','w','h'],"Images/rect_prism.png","calc_rprism_sa"]

Line 4 shows the configuration for cube. The string inside the first pair of square brackets is the name of the shape as presented in the tool. After the equal symbol, the list of variables, the name of the image file, and finally the name of the calculation function are given.
Line 5 shows a similar configuration for rectangular prisms. In this case the user will be required to enter values for three variables representing the length, width and height respectively.

Measurement Toolkit (part 2)

Jun2

Unit conversions

In the first step of the Measurement toolkit tutorial we downloaded the initial source code and installed the pillow package. In this step we will complete the functionality and testing for the unit conversion part of the tool. This will consist of conversions for metric units for length, area and volume.

Testing length conversions

We begin by considering conversions for metric units of length. The following diagram shows the process for converting between the four most widely used units (millimetres, centimetres, metres and kilometres).

Converting metric units of length

To perform a conversion we follow the arrows from the initial unit to the target unit, applying the operation attached to each arc.
Conversion calculations are firstly written by hand – these will then form the basis for test cases. For example, calculations for converting kilometres to millimetres are shown below.

$1.2\mathrm{km}=1.2 \times 1000 = 1200\mathrm{m}$
$1200\mathrm{m} = 1200 \times 100 = 120000\mathrm{cm}$
$120000\mathrm{cm}=120000 \times 10 = 1200000\mathrm{mm}$

Once calculations have been done to cover all of the metric length unit conversions they should be coded in the convert_units_tester.py file. The existing code for this is shown below. Test cases for converting from metres have already been included. The highlighted code (lines 6 and 7) contains a function to test whether the conversion from metres to millimetres is correct.
Each test case function begins with the keyword def followed by the name of the function, in this case test_m_to_mm, finally we include the input variable self in brackets followed by a colon. The first line of each test case function will the same except the function name will differ – ensure you give a meaningful name and make sure each function has a different name. The second line of the function contains the actual test case. The assertEqual function takes two arguments. The first argument on line 7 calls the convert_length_unit function and returns a result. The second argument contains the expected (correct) result. If the first argument equals the second argument then the test passes. Otherwise the test fails, indicating that we probably have an error in the code in the convert_length_unit in the file convert_units.py.

import unittest
from convert_units import *

class TestConvertUnits(unittest.TestCase):

    def test_m_to_mm(self):
        self.assertEqual(convert_length_unit(0.23,"m","mm"),230)
    def test_m_to_cm(self):
        self.assertEqual(convert_length_unit(0.25,"m","cm"),25)
    def test_m_to_m(self):
        self.assertEqual(convert_length_unit(178,"m","m"),178)
    def test_m_to_km(self):
        self.assertEqual(convert_length_unit(19000,"m","km"),19)

if __name__ == '__main__':
    unittest.main()

The tester code imports the code in convert_units.py on line 2, which contains the conversion functions. We will look at this file in more detail a little later. Before we do so we must complete the length unit conversion tests in convert_units_tester.py file.

For example, to add a test based on the kilometre to millimetre calculation shown earlier we would add the following code.

    def test_km_to_mm(self):
        self.assertEqual(convert_length_unit(1.2,"km","mm"),1200000)

This code would be included immediately after the previous test functions, making sure it is indented to the same level as the other test functions.
When the tester code is run it creates a report on how many tests passed or failed. The ultimate aim is obviously to pass all tests.
To ensure that all functionality is tested we should have at least one test case for each possible conversion, including conversions from a unit to itself (e.g. from metres to metres).
This means that you will need to write at least sixteen (16) length conversion tests.

When you run your length conversion tests you should get a number of failed tests – these represent errors in the convert_length_unit code. As mentioned the code for this function is given in the convert_units.py file and is listed below. Running the tests should help you identify the errors in the code. These should be corrected and tests should be rerun to ensure the function is free of errors.

def convert_length_unit(value,inunit, outunit):
    if (inunit==outunit):
        result=value
    elif (inunit=="m") & (outunit=="mm"):
        result=value*1000
    elif (inunit=="m") & (outunit=="cm"):
        result=value*10
    elif (inunit=="m") & (outunit=="km"):
        result=value*1000
    elif (inunit=="km") & (outunit=="mm"):
        result=value*1000000
    elif (inunit=="km") & (outunit=="cm"):
        result=value*10000
    elif (inunit=="km") & (outunit=="m"):
        result=value*1000
    elif (inunit=="cm") & (outunit=="mm"):
        result=value*100
    elif (inunit=="cm") & (outunit=="m"):
        result=value/100
    elif (inunit=="cm") & (outunit=="km"):
        result=value/100*1000
    elif (inunit=="mm") & (outunit=="cm"):
        result=value/10
    elif (inunit=="mm") & (outunit=="m"):
        result=value/1000
    elif (inunit=="mm") & (outunit=="km"):
        result=value/1000*1000
    return result

The function takes three input arguments, the first is the numerical value to be converted, the second is the original units of the measurement, and the third is the target units of the measurement. The function is implemented using a nested if-then-else statement. At the end of the function the converted measurement is returned as the result.

Area conversions

The next step is to develop the area unit conversions.
If you are doing this part of the development in pairs, then one person should design and develop the test cases in convert_units_tester.py, while the second person writes the area conversion function in convert_units.py

The diagram below shows the conversion process for units of area.

Area unit conversions

For example, consider the following conversion calculation:
$5.8\mathrm{m^2} = 5.8 \times 100^2= 58000 \mathrm{cm^2}$
$58000\mathrm{cm^2}=58000 \times 10^2 = 5800000 \mathrm{mm^2}$

This process can be repeated on paper to design test cases for each of the 16 possible area conversions (remember we need to include tests that check that conversions for a unit to itself leave the value unchanged). Once the test cases have been calculated on paper they can be added to the convert_units_tester.py file. The should be added immediately after the length unit test functions. For example, the test case calculated above would be written as:

    def test_m2_to_mm2(self):
        self.assertEqual(convert_area_unit(5.8, "m2", "mm2"), 5800000)

Notice that the test function name indicates that units of area are being converted – don’t forget to include the correct units in the function name. The test is implemented by calling the assertEqual function. This in turn calls convert_area_unit which takes three arguments – the original area measurement, the original units of area and the target units of area. The units of area include a 2 at the end to distinguish them from units of length.

The last step in the process is to write the code for the convert_area_unit function, contained in the
convert_units.py file. In the supplied code this function is written as a code stub, meaning that the function is defined, but it is not implemented correctly. In this case the function stub returns 0 regardless of the inputs to the function as shown below.

def convert_area_unit(value,inunit,outunit):
    return 0

The second line of the function needs to be replaced by code similar to that given for the convert_length_unit function, remembering though that the units of area will all need to include a 2 at the end. To implement this function, you should use the earlier area conversion diagram as a guide.

Once the code for the convert_area_unit function has been written, then you should test it by running the test cases in convert_units_tester.py.

Volume conversions

The last step in completing the unit conversions for the Measurement toolkit is to add volume conversions. As with the area conversions, if you are working in pairs one person should work on designing and implementing the test cases, while the other person develops the conversion code. For this task however you should swap roles.

Volume conversions

The calculations for an example conversion is shown below:
$19500000\mathrm{mm^3}=19500000 \div 10^3 = 19500 \mathrm{cm^3}$
$19500\mathrm{cm^3} = 19500 \div 100^3 = 0.0195 \mathrm{m^3}$

Calculations should be completed for all 16 possible conversions. These test cases should then be implemented in the convert_units_tester.py file.
The conversion functionality is added to the tool by implementing the following code stub in
the convert_units.py file, replacing the second line with appropriate code.

def convert_volume_unit(value,inunit,outunit):
    return 0

Measurement Toolkit (part 1)

Jun2

Introduction

In this series of tutorials we explain how to develop a Measurement toolkit which provides functions for converting units of measurement and calculating the surface area and volume of a range of 3d shapes.

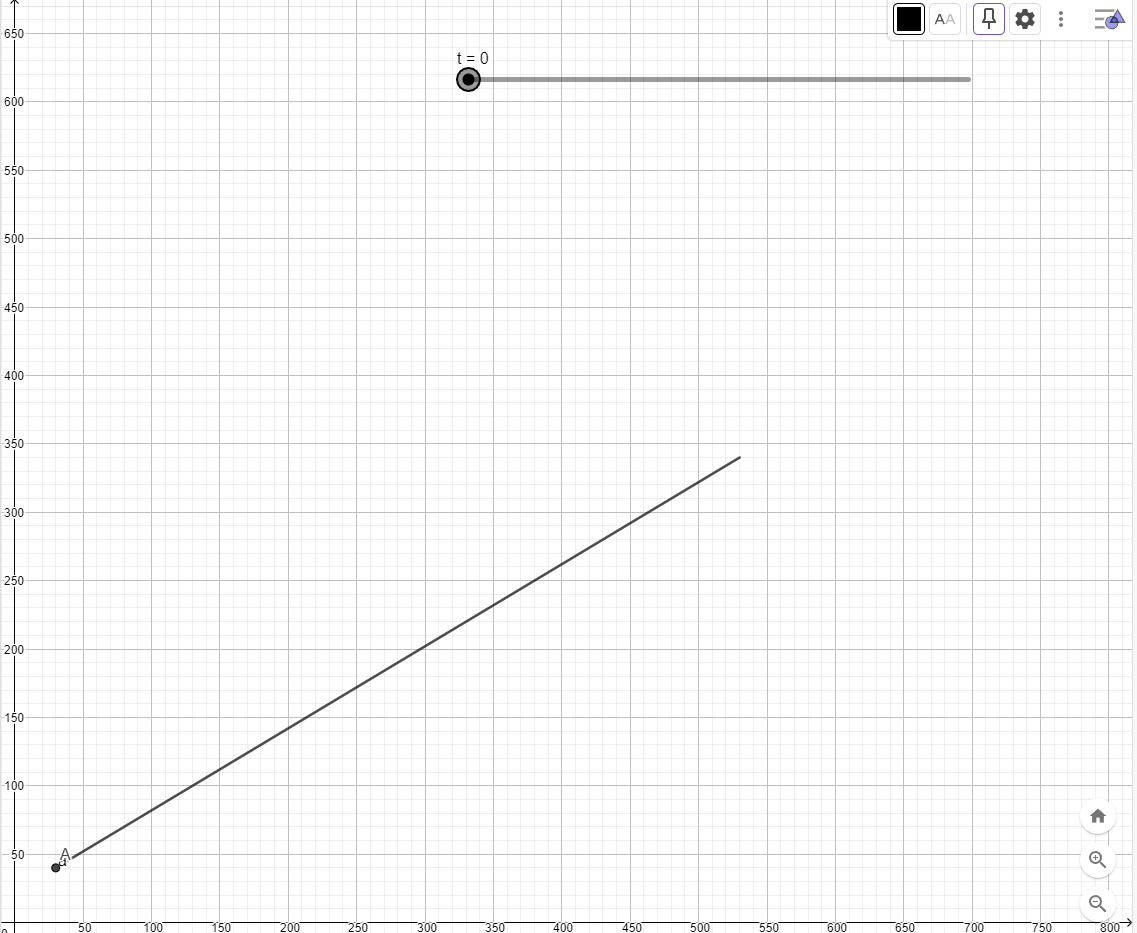
A screenshot showing the Measurement toolkit is given below showing the unit conversion capabilities of the tool.

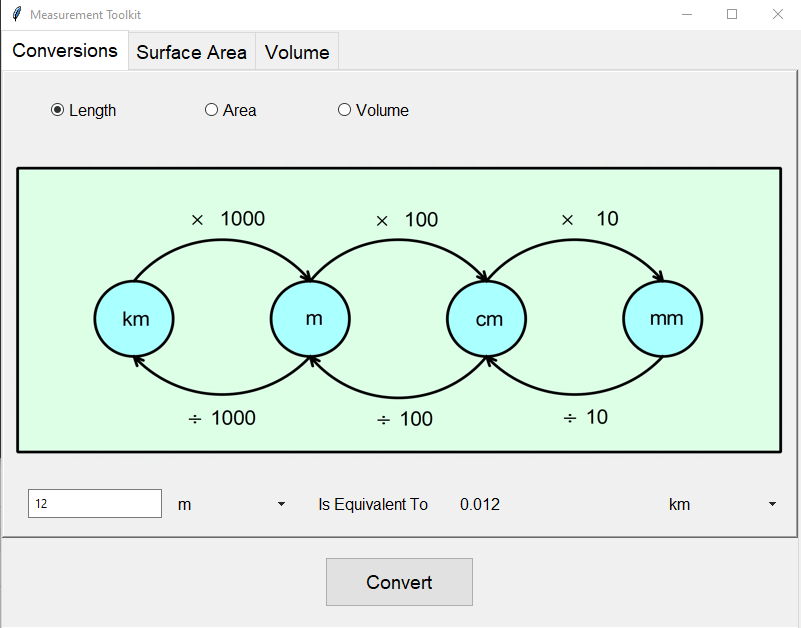
Unit conversions in the Measurement Toolkit

Initial setup

The starting point for the development of the Measurement Toolkit is to download the initial source code files for the Measurement Toolkit. This zip file should be downloaded and extracted to a suitable location. These files provide the basic skeletal code for the application. It includes graphical user interface (GUI) code, together with stubs for the functions that do the conversions and calculations.

The files are listed below, with full code listings that can be expanded and view. We will describe each of these files in more detail in later parts of this tutorial as required.

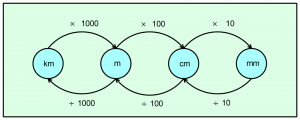
convert_units.py – will contain functions for carrying out unit conversions. Code is provided in this file for converting units of length, however several errors have been included which need to be found through testing and fixed. Stubs (incomplete functions) for converting area and volume units are also given.

def convert_length_unit(value,inunit, outunit):
    if (inunit==outunit):
        result=value
    elif (inunit=="m") & (outunit=="mm"):
        result=value*1000
    elif (inunit=="m") & (outunit=="cm"):
        result=value*10
    elif (inunit=="m") & (outunit=="km"):
        result=value*1000
    elif (inunit=="km") & (outunit=="mm"):
        result=value*1000000
    elif (inunit=="km") & (outunit=="cm"):
        result=value*10000
    elif (inunit=="km") & (outunit=="m"):
        result=value*1000
    elif (inunit=="cm") & (outunit=="mm"):
        result=value*100
    elif (inunit=="cm") & (outunit=="m"):
        result=value/100
    elif (inunit=="cm") & (outunit=="km"):
        result=value/100*1000
    elif (inunit=="mm") & (outunit=="cm"):
        result=value/10
    elif (inunit=="mm") & (outunit=="m"):
        result=value/1000
    elif (inunit=="mm") & (outunit=="km"):
        result=value/1000*1000
    return result

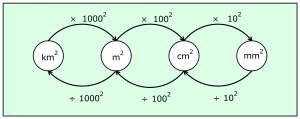
def convert_area_unit(value,inunit,outunit):
    return 0

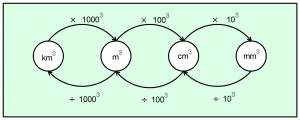
def convert_volume_unit(value,inunit,outunit):
    return 0

convert_units_tester.py – will contain test cases to check the correctness of the unit conversion functions. Test cases have been written for converting from metres to other units. Using the same syntax you will be required to complete the other test cases.

import unittest
from convert_units import *

class TestConvertUnits(unittest.TestCase):

    def test_m_to_mm(self):
        self.assertEqual(convert_length_unit(0.23,"m","mm"),230)
    def test_m_to_cm(self):
        self.assertEqual(convert_length_unit(0.25,"m","cm"),25)
    def test_m_to_m(self):
        self.assertEqual(convert_length_unit(178,"m","m"),178)
    def test_m_to_km(self):
        self.assertEqual(convert_length_unit(19000,"m","km"),19)

if __name__ == '__main__':
    unittest.main()

mathtoolkit.py – the main program file, containing of the GUI code and user configurable code allowing additional shapes to be added to the surface area and volume calculator parts of the tool

from tkinter import *
from tkinter import ttk
from convert_units import *
from surface_area import *
from volume import *
from PIL import Image,ImageTk
import math


def convert_units_and_display():
    if (unitsvar.get()==1):
        converted=convert_length_unit(float(unitval.get()),funitvar.get(),tunitvar.get())
    elif (unitsvar.get()==2):
        converted=convert_area_unit(float(unitval.get()),funitvar.get(),tunitvar.get())
    elif (unitsvar.get()==3):
        converted=convert_volume_unit(float(unitval.get()),funitvar.get(),tunitvar.get())
    convertedval.set(str(converted))
    
def change_unit_options():
    m1=foptnmenu['menu']
    m1.delete(0,END)
    m2=toptnmenu['menu']
    m2.delete(0,END)
    
    if (unitsvar.get()==2):
        newvalues=['mm2','cm2','m2','km2']
        funitvar.set("m2")
        tunitvar.set("m2")
        image=Image.open("Images/area_convert.png").resize((780,300))
        img=ImageTk.PhotoImage(image)
        cimage_label.configure(image=img)
        cimage_label.image=img

    elif(unitsvar.get()==3):
        newvalues=['mm3','cm3','m3','km3']
        funitvar.set("m3")
        tunitvar.set("m3")
        image=Image.open("Images/volume_convert.png").resize((780,300))
        img=ImageTk.PhotoImage(image)
        cimage_label.configure(image=img)
        cimage_label.image=img
    else:
        newvalues=['mm','cm','m','km']
        funitvar.set("m")
        tunitvar.set("m")
        image=Image.open("Images/length_convert.png").resize((780,300))
        img=ImageTk.PhotoImage(image)
        cimage_label.configure(image=img)
        cimage_label.image=img

    
    for val in newvalues:
        m1.add_command(label=val,command=lambda v=funitvar,l=val:funitvar.set(l))
        m2.add_command(label=val,command=lambda v=tunitvar,l=val:tunitvar.set(l))


def display_shape_sa(self):
    sproperties=sa_shapes[shapevar.get()]
    refresh_surface_area(sproperties[0],
                         sproperties[1])
    

def calc_surface_area():
    arglist=""
    for i in range(0,len(valarray)-1):
        arglist=arglist+"{0},".format(valarray[i].get())
    arglist=arglist+"{0}".format(valarray[len(valarray)-1].get())
    answer=(eval(sa_shapes[shapevar.get()][2]+"("+arglist+")"))
    sa_text.set("Surface Area of {0} is {1:.2f} units^2".format(shapevar.get(),answer))
    
    


def refresh_surface_area(varlist,imageloc):
    valarray.clear()
    for l in range(0,len(varlabels)):
        varlabels[l].destroy()
    for l in range(0,len(varentries)):
        varentries[l].destroy()
    for i in range(0,len(varlist)):
        valarray.append(StringVar(main))
        lab=ttk.Label(vframe,text="{0}=".format(varlist[i]))
        lab.grid(row=i+1,column=0,pady=20,sticky=W)
        varlabels.append(lab)
        entry=ttk.Entry(vframe,width=20,textvariable=valarray[i])
        entry.grid(row=i+1,column=1,sticky=W)
        varentries.append(entry)
    image=Image.open(imageloc).resize((400,400))
    img=ImageTk.PhotoImage(image)
    image_label.configure(image=img)
    image_label.image=img

def display_shape_vol(self):
    vproperties=vol_shapes[vshapevar.get()]
    refresh_volume(vproperties[0],
                    vproperties[1])
    

def calc_volume():
    arglist=""
    for i in range(0,len(vvalarray)-1):
        arglist=arglist+"{0},".format(vvalarray[i].get())
    arglist=arglist+"{0}".format(vvalarray[len(vvalarray)-1].get())
    answer=(eval(vol_shapes[vshapevar.get()][2]+"("+arglist+")"))
    vol_text.set("Volume of {0} is {1:.2f} units^3".format(vshapevar.get(),answer))
    
    


def refresh_volume(varlist,imageloc):
    vvalarray.clear()
    for l in range(0,len(vvarlabels)):
        vvarlabels[l].destroy()
    for l in range(0,len(vvarentries)):
        vvarentries[l].destroy()
    for i in range(0,len(varlist)):
        vvalarray.append(StringVar(main))
        lab=ttk.Label(vframe2,text="{0}=".format(varlist[i]))
        lab.grid(row=i+1,column=1,pady=20)
        vvarlabels.append(lab)
        entry=ttk.Entry(vframe2,width=20,textvariable=vvalarray[i])
        entry.grid(row=i+1,column=2)
        vvarentries.append(entry)
    image=Image.open(imageloc).resize((400,400))
    img=ImageTk.PhotoImage(image)
    vimage_label.configure(image=img)
    vimage_label.image=img
####################
## Top level GUI setup
######################

main=Tk()
main.title('Measurement Toolkit')
main.geometry('800x600')
rows=0

main.grid_rowconfigure(0, weight=1)
main.grid_columnconfigure(0, weight=1)

style = ttk.Style(main)
style.configure('TRadiobutton', font=('Helvetica', 12))
style.configure('TNotebook.Tab', font=('Helvetica', 14), padding=5)
style.configure('TButton', font=('Helvetica', 14), padding=10)
style.configure('TLabel', font=('Helvetica', 12))
style.configure('TEntry', font=('Helvetica', 12), padding=5)
style.configure('TMenubutton', font=('Helvetica', 12), padding=5)

nb=ttk.Notebook(main)



nb.grid(row=0,sticky="nesw")



page1=ttk.Frame(nb)
nb.add(page1,text='Conversions')
page2=ttk.Frame(nb)
nb.add(page2,text='Surface Area')
page3=ttk.Frame(nb)
nb.add(page3,text='Volume')

##################
## Conversions
###################
page1.rowconfigure(0,weight=2)
page1.rowconfigure(1,weight=1)
page1.columnconfigure(0,weight=1,uniform=1)
unitsvar=IntVar()
unitsvar.set(1)


cframe=ttk.Frame(page1,relief=RAISED,padding=5)
cframe.grid(row=0,column=0,sticky="nesw")
cframe.columnconfigure((0,1,2,3,4),weight=1)
cframe.rowconfigure(1,weight=1)
cframe.rowconfigure((0,2),weight=1)


cimage_label=ttk.Label(cframe)
cimage_label.grid(row=1,column=0,columnspan=5,sticky="ew")
image=Image.open("Images/length_convert.png").resize((780,300))
img=ImageTk.PhotoImage(image)
cimage_label.configure(image=img)
cimage_label.image=img

ttk.Radiobutton(cframe,text="Length",variable=unitsvar,value=1,command=change_unit_options).grid(row=0,column=0,pady=10)
ttk.Radiobutton(cframe,text="Area",variable=unitsvar,value=2,command=change_unit_options).grid(row=0,column=1,pady=10)
ttk.Radiobutton(cframe,text="Volume",variable=unitsvar,value=3,command=change_unit_options).grid(row=0,column=2,pady=10)

funitvar=StringVar(main)
tunitvar=StringVar(main)
unitchoices=['mm','cm','m','km']




unitval=StringVar(main)
unitval.set("0")
convertedval=StringVar(main)
convertedval.set("0")
ttk.Label(cframe,text='Is Equivalent To').grid(row=2,column=2,padx=5,pady=5)
uentry=ttk.Entry(cframe,width=20,textvariable=unitval)
uentry.grid(row=2,column=0,sticky='E')
foptnmenu=ttk.OptionMenu(cframe,funitvar,'m',*unitchoices)
foptnmenu.configure(width=10)
foptnmenu.grid(row=2,column=1)
convertLabel=ttk.Label(cframe,textvariable=convertedval,width=20)
convertLabel.grid(row=2,column=3)
toptnmenu=ttk.OptionMenu(cframe,tunitvar,'m',*unitchoices)
toptnmenu.configure(width=10)
toptnmenu.grid(row=2,column=4)
convertButton=ttk.Button(page1,text="Convert",
                     command=convert_units_and_display)
convertButton.grid(row=1,column=0)

#################
## Surface Area
###################
sa_shapes={}

##
## ADD NEW SHAPES HERE FOR SURFACE AREA
##
sa_shapes['Cube']=[['l'],"Images/cube.png","calc_cube_sa"]
sa_shapes['Rectangular Prism']=[['l','w','h'],"Images/rect_prism.png","calc_rprism_sa"]




##
## DO NOT EDIT BELOW HERE
##

page2.rowconfigure(0,weight=1)
page2.rowconfigure(1,weight=1)
page2.rowconfigure(2,weight=1)
page2.rowconfigure(3,weight=1)
page2.columnconfigure(0,weight=1,uniform=1)

shapechoices=sa_shapes.keys()
shapevar=StringVar(main)
shapevar.set('Cube')

shapeoptnmenu=ttk.OptionMenu(page2,shapevar,"Cube",*shapechoices,command=display_shape_sa)
shapeoptnmenu.configure(width=30)
shapeoptnmenu.grid(row=0,column=0,sticky=W)
vframe=ttk.Frame(page2,relief=RAISED,padding=10)
vframe.grid(row=1,column=0,sticky=NSEW)




ttk.Label(vframe,text="Variables").grid(row=0,column=1,padx=20)
iframe=ttk.Frame(page2,relief=RAISED,padding=5)
iframe.grid(row=1,column=1,sticky=NSEW)
valarray=[]
varlabels=[]
varentries=[]
image_label=ttk.Label(iframe,background='white')
image_label.grid(row=0,column=0)
display_shape_sa(main)


sa_text=StringVar()
sa_text.set("Press Calculate button")
ttk.Label(page2,textvariable=sa_text).grid(row=2,column=0, columnspan=2, sticky=W)
ttk.Button(page2,text="Calculate",command=calc_surface_area).grid(row=3,column=0,columnspan=2)


################
## Volume
################
vol_shapes={}
##
## ADD NEW SHAPES HERE FOR VOLUME
##
vol_shapes['Cube']=[['l'],"Images/cube.png","calc_cube_vol"]
vol_shapes['Rectangular Prism']=[['l','w','h'],"Images/rect_prism.png","calc_rprism_vol"]

##
## DO NOT EDIT BELOW HERE
##
page3.rowconfigure(0,weight=1)
page3.rowconfigure(1,weight=1)
page3.rowconfigure(2,weight=1)
page3.rowconfigure(3,weight=1)
page3.columnconfigure(0,weight=1,uniform=1)
vshapechoices=vol_shapes.keys()
vshapevar=StringVar(main)
vshapevar.set('Cube')

vshapeoptnmenu=ttk.OptionMenu(page3,vshapevar,"Cube",*vshapechoices,command=display_shape_vol)
vshapeoptnmenu.configure(width=30)
vshapeoptnmenu.grid(row=0,column=0,sticky=W)
vframe2=ttk.Frame(page3,relief=RAISED)
vframe2.grid(row=1,column=0,sticky=NSEW)

ttk.Label(vframe2,text="Variables").grid(row=0,column=1,columnspan=2,padx=20)
iframe2=ttk.Frame(page3,relief=RAISED,padding=5)
iframe2.grid(row=1,column=1,sticky=NSEW)
vvalarray=[]
vvarlabels=[]
vvarentries=[]
vimage_label=ttk.Label(iframe2,background='white')
vimage_label.grid(row=0,column=0)
display_shape_vol(main)

vol_text=StringVar()
vol_text.set("Press Calculate button")
ttk.Label(page3,textvariable=vol_text).grid(row=2,column=0, columnspan=2, sticky=W)
ttk.Button(page3,text="Calculate",command=calc_volume).grid(row=3,column=0,columnspan=2)

main.mainloop()

surface_area.py – will contain the functions for calculating the surface area of various 3d shapes

import math

def calc_cube_sa(length):
    return 6*(length)**2

def calc_rprism_sa(length,width,height):
    return 0

surface_area_tester.py – will contain test cases to check the correctness of the surface area calculation functions

import unittest
from surface_area import *

class TestSurfaceArea(unittest.TestCase):
    def test_calc_cube_sa(self):
        self.assertEqual(calc_cube_sa(5),150)
        self.assertAlmostEqual(calc_cube_sa(3.275),64.35,2)

if __name__ == '__main__':
    unittest.main()

volume.py – will contain the functions for calculating the volume of various 3d shapes

import math

def calc_cube_vol(l):
    return l**3

def calc_rprism_vol(l,w,h):
    return 0

volume_tester.py – will contain test cases to check the correctness of the volume calculation functions

import unittest
from volume import *

class TestVolume(unittest.TestCase):
    def test_calc_cube_vol(self):
        self.assertEqual(calc_cube_vol(5),125)

if __name__ == '__main__':
    unittest.main()

Images – stores the image files that will be used to represent the 3d shapes, together with the unit conversion diagrams

To run the program you will also need to install the pillow package in Python using the following command:
pip install pillow pip --trusted-host pypi.org --trusted-host files.pythonhosted.org

Quadratic Iteration in the TI-84

Sep6

Quadratic iteration is used to generate the Mandelbrot set and Julia sets. An image of Mandelbrot set is shown below.

Mandelbrot Set

Consider the following quadratic iteration

$z \to z^2+(0.5+0.2i)$

Given an initial value of

$z_0=0$

This can be done in the TI-84 by storing the initial value in the variable Z and storing the constant in the variable C.

New values can be generated by applying the iterative rule shown above. Applying this operation repeatedly generates a sequence of values.

$z_1 = 0^2+(0.5+0.2i) = 0.5+0.2i$

The second iteration leads to

$z_2 = (0.5+0.2i)^2+(0.5+0.2i) = 0.71+0.4i$

This is done in the TI-84 by assigning the expression Z²+C to the variable Z.

While the third iteration leads to the following value:

$z_3 = (0.71+0.4i)^2+(0.5+0.2i) = 0.8441+0.768i$

Completing these calculations by hands is tedious and error prone. The process can be simplified greatly using a program in the TI-84.

Below is a video demonstrating how to write a program for doing quadratic iteration in the TI-84.

$\displaystyle \begin{array}{l}x_1=x_2+3\\\int{x\hat{\ }2dx=\frac{x\hat{\ }3}{3}+c}\end{array}$

Digital Technology

Technology for the 21st century and beyond

Category Archives: Mathematics

Asteroids Simulator

Step 1: Screen dimensions

Step 2: Representing time

Step 3: Modelling a missile

Step 4: Modelling an asteroid

Step 5: Tracking the distance between objects

Extra bling

Investigating Trigonometric Ratios

Investigating similar triangles using Geogebra

Measurement Toolkit (part 3)

Surface area calculator

Designing test cases

Coding the surface area calculation functions

Creating 3d shapes

Linking the components in the main interface

Measurement Toolkit (part 2)

Unit conversions

Testing length conversions

Area conversions

Volume conversions

Measurement Toolkit (part 1)

Introduction

Initial setup

Quadratic Iteration in the TI-84

Subscribe By Email

	Angle	Opp	Adj	Hyp	$\dfrac{Opp}{Adj}$	$\dfrac{Opp}{Hyp}$	$\dfrac{Adj}{Hyp}$
Triangle 1
Triangle 2
Triangle 3

	Angle 1	Angle 2	Angle 3
Triangle 1
Triangle 2

	Side 1	Side 2	Side 3	Side 1 ÷ Side 2	Side 1 ÷ Side 3	Side 2 ÷ Side 3
Triangle 1
Triangle 2