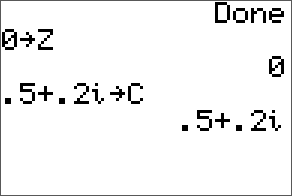This article explains how to develop a simulator of part of an Asteroids game in Geogebra using parametric curves based on position vectors. Note that this simulator is intended for exploring mathematical models and as such many of the details of a full Asteroids game have been abstracted.
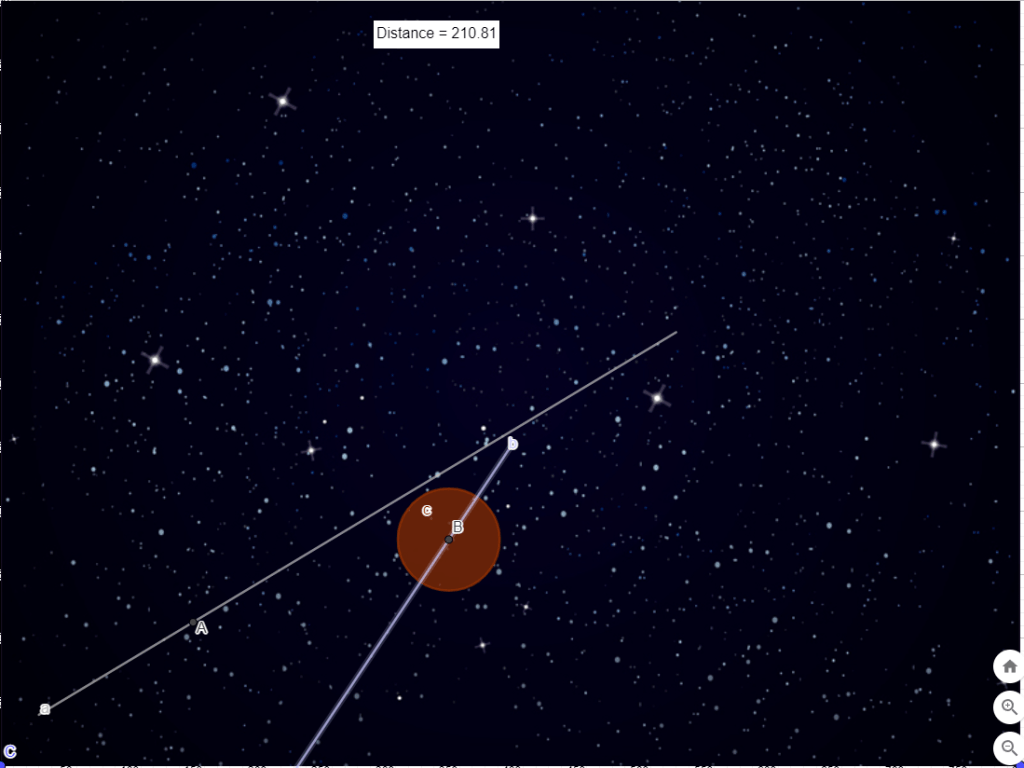
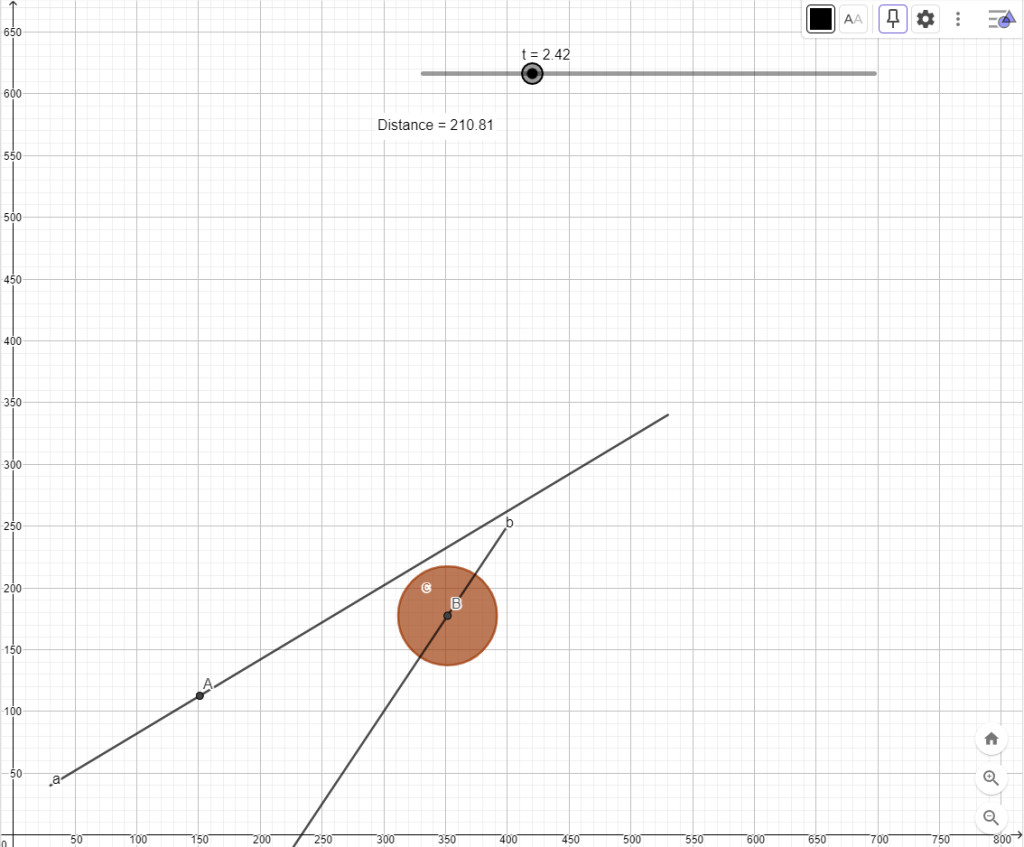
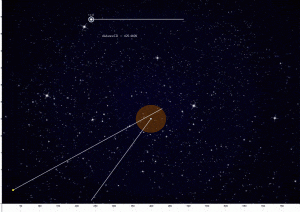
The animated gif image below is an example of a simple simulator developed in Geogebra. The large circle represents an Asteroid, while the smaller circle (dot) represents a missile that has been fired. The simulator demonstrates whether or not the missile hits the Asteroid and can be used to determine the minimum distance between the centre of the Asteroid and the missile.
Before we create the simulator, we provide a brief description of the main components of the Geogebra tool.
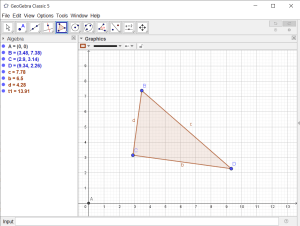
The screenshot below shows Geogebra Classic 6. On the left-hand side is the Algebra window. This is where we will input components of the mathematical model, including curves and points. The middle and main part of the display is the Graphic window, this is where the asteroids model will be displayed. The toolbar at the top of the screen provide access to the main geometric tools – in this article we some of these tools to create a slider, create a circle to represent an asteroid and add text showing the distance between two points.
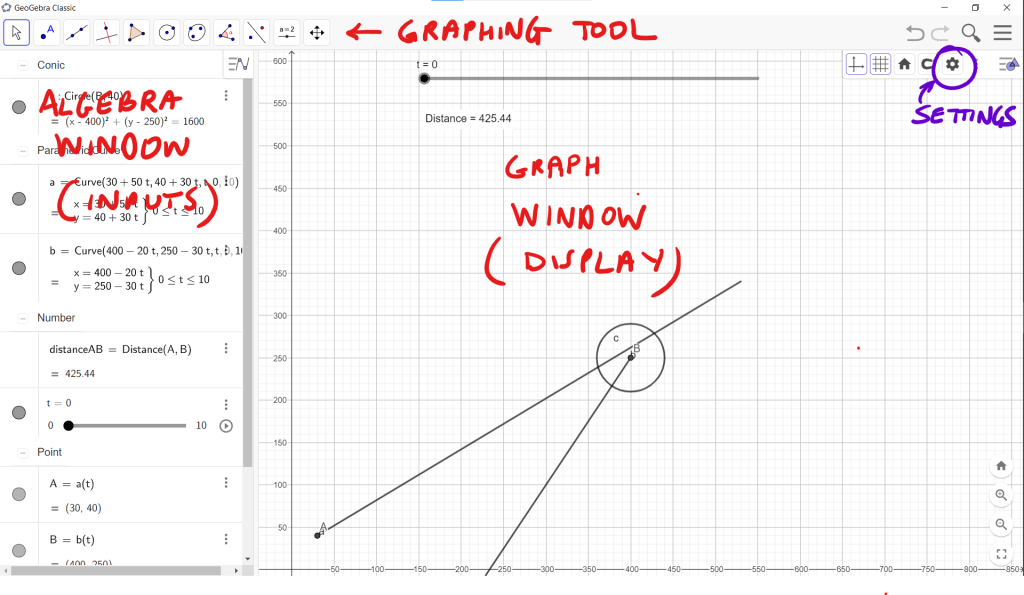
The highlighted settings button allows for the configuration of elements on the Graph window. Clicking on the background allows us to configure the background window.
Step 1: Screen dimensions
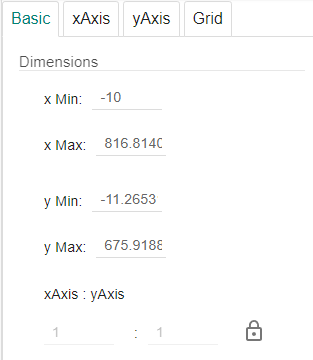
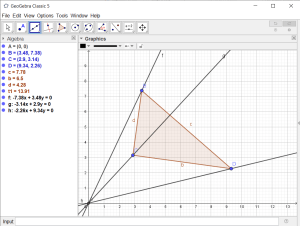
We begin by setting the screen dimensions. We assume that the game is played on a 4:3 aspect ratio with a resolution of 800 pixels wide and 600 pixels high. In Geogebra we will let 1 unit represent 1 pixel in the game. As such the range of x values will be between 0 and 800, while the range of y values will be between 0 and 600. Settings for this in Geogebra are shown below. Note that maximum x and y values go slightly beyond the range. Note also that we have a 1:1 ratio between the x and y scales. To access the configuration options for the background, click on the settings button.
Step 2: Representing time
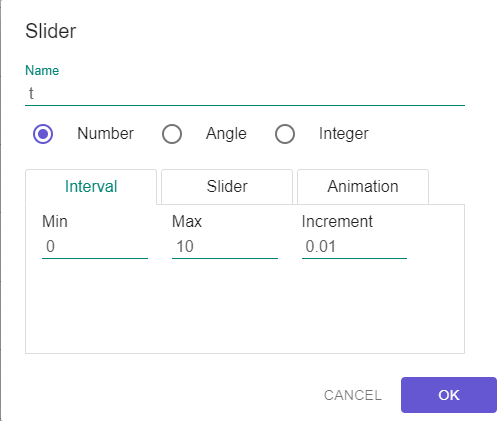
Time (in seconds) will be represented using a slider. For our example time will range from 0 to 10 seconds, with increments of 0.01 seconds. This slider is created using the slider tool.
![]()
The configuration options are shown in the following image.
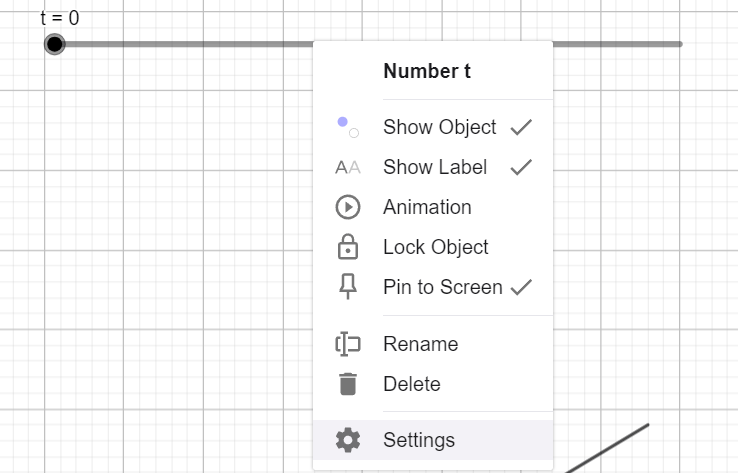
The width of the slider is increased from the default of 200 pixels to 500 pixels. To configure this right-click on the slider and select “Settings”.
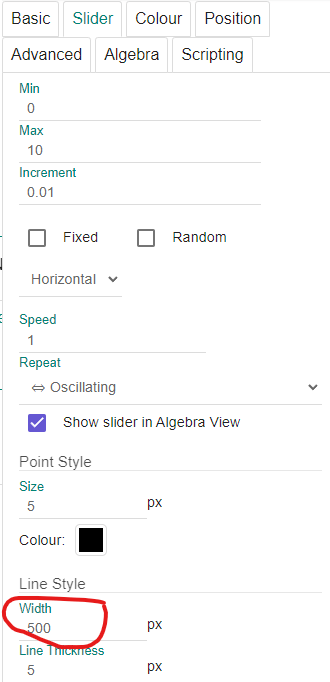
The settings window for the slider is shown below with the updated width value highlighted.
Step 3: Modelling a missile
The missile in our example has an initial position of (30, 40) and a velocity vector of [50, 30]. The position vector (relative to the origin) is given as follows.
To represent this position vector in Geogebra we use the Curve function. The function takes parameterised expressions for the x-coordinates and y-coordinates of points on the curve, together with parameter used in the expressions, and the lower and upper limits of values passed to the parameter. In this case we use the variable t as the parameter and set the range of values from 0 to 10. The input for this in Geogebra is as follows:
Curve(30+50t, 40+30t, t, 0, 10)
To trace the path of the missile at a particular time we create a new point representing the point on the curve for the current value of the time variable. The input for this in Geogebra is given below:
a(t)
The details of the curve and parameterised point should appear in Geogebra as shown in the screenshot below.
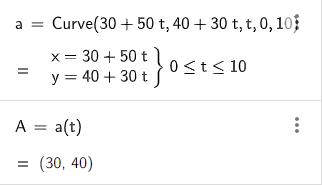
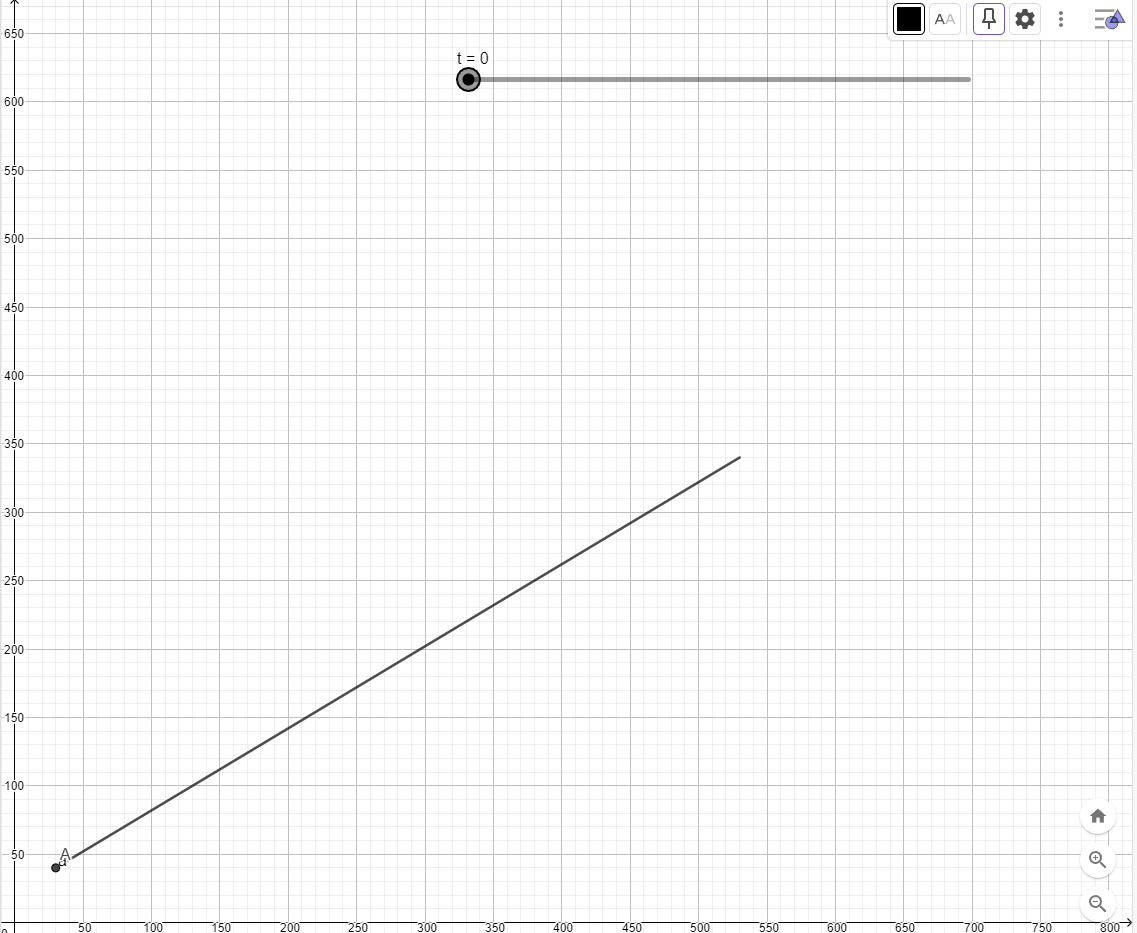
The graphing window should look like the screenshot below after the commands shown above have been entered. It shows the path that the missile will take over the 10 second time interval, together with the current position of the missile (shown as point A). The time variable has a value of 0 and the missile is at its starting position of (30, 40).
Step 4: Modelling an asteroid
Next we model an asteroid with an initial position of (400, 250) and a velocity vector of [-20, -30]. The asteroid will be modelled as a circle with a diameter of 80 pixels. The position vector (relative to the origin) of the asteroid is given as follows.
The path of the asteroid is modelled using the Curve function in Geogebra.
Curve(400-20t, 250-30t, t, 0, 10)
Next, the centre of the asteroid is modelled as a parameterised point.
b(t)
Finally, a circle whose centre is the parameterised point is created using the “Circle: Center and Radius” tool.
![]()
The radius of the circle is 40 pixels. The details of the curve, parameterised point and circle are shown in the screenshot below.
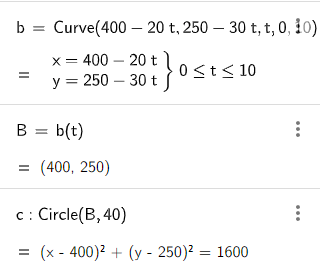
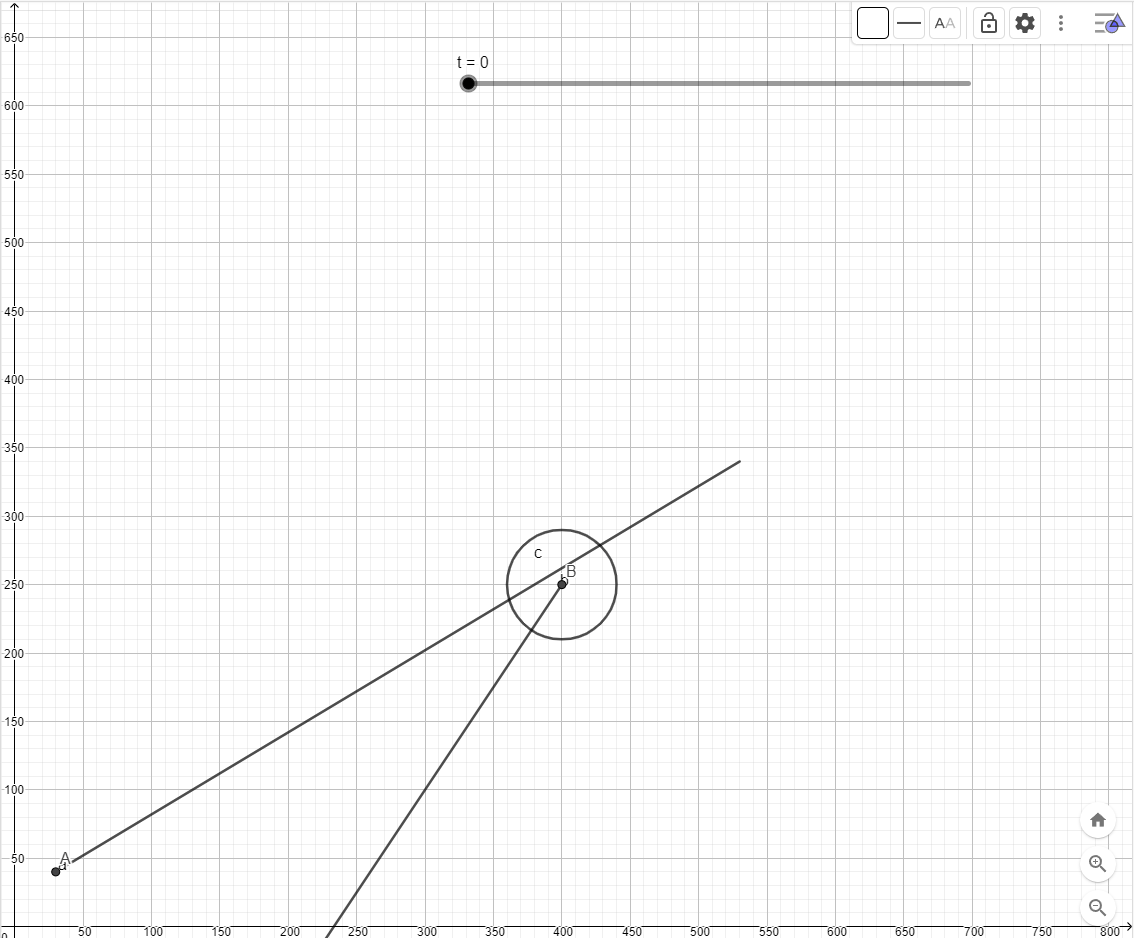
After these commands have been added the graphing window should look like the screenshot below.
Step 5: Tracking the distance between objects
To determine whether the missile hits the asteroid we will track the distance between the centres of these objects. We begin by choosing the “Distance or Length” tool and selecting the point representing the missile and the point representing the centre of the asteroid (points A and B). This will create a distance calculation object together with a text object to display the distance.
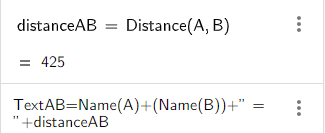
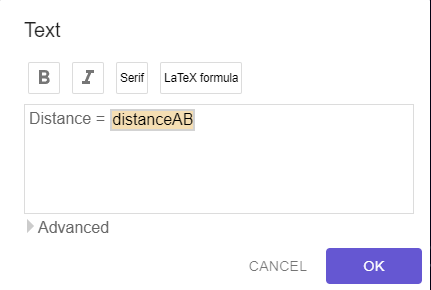
Double-clicking on the text element pops up a window allowing us to edit the text. In this case we change the text on the left-hand side of the equal sign as shown in the screenshot below.
We then open the settings for the text object and click on the Pin to Screen option. Selecting this lets us move the text to the top of the screen.
After these steps have been completed the Graphic Window will look like the screenshot below (note this also includes a change in colour for the asteroid which is accessed by clicking on the asteroid object and then selecting settings).
Extra bling
The look of the simulator can be improved by adding a space background. This is done by choosing the “Image” tool.
![]()
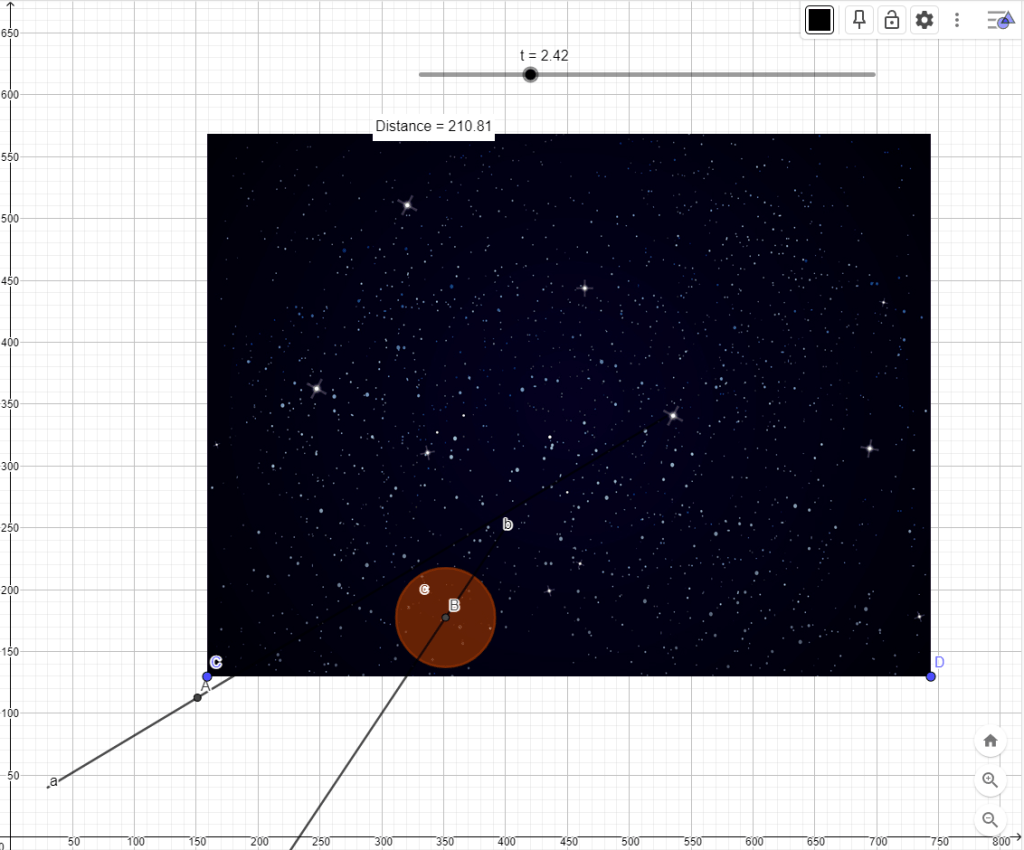
In this case an image that has the correct 4:3 aspect ratio is chosen. The image appears in the middle of the Graph window as shown in the following screenshot.
The anchor points of the image (points C and D) are so that the image covers an 800×600 area.

The final result is shown in the following screenshot.