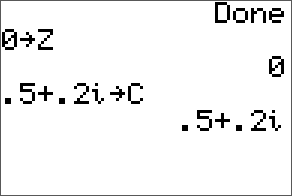Tag Archives: TI84

Quadratic Iteration in the TI-84

Quadratic iteration is used to generate the Mandelbrot set and Julia sets. An image of Mandelbrot set is shown below.

Mandelbrot Set

Mandelbrot Set

Consider the following quadratic iteration

z \to z^2+(0.5+0.2i)

Given an initial value of

z_0=0

This can be done in the TI-84 by storing the initial value in the variable Z and storing the constant in the variable C.

Capture 1

New values can be generated by applying the iterative rule shown above. Applying this operation repeatedly generates a sequence of values.

z_1 = 0^2+(0.5+0.2i) = 0.5+0.2i

The second iteration leads to

z_2 = (0.5+0.2i)^2+(0.5+0.2i) = 0.71+0.4i

This is done in the TI-84 by assigning the expression Z²+C to the variable Z.

Capture 4

While the third iteration leads to the following value:

z_3 = (0.71+0.4i)^2+(0.5+0.2i) = 0.8441+0.768i

Capture 5

Completing these calculations by hands is tedious and error prone. The process can be simplified greatly using a program in the TI-84.

Below is a video demonstrating how to write a program for doing quadratic iteration in the TI-84.

 

\displaystyle \begin{array}{l}x_1=x_2+3\\\int{x\hat{\ }2dx=\frac{x\hat{\ }3}{3}+c}\end{array}