To explore properties of similar triangles we will apply enlargement transformations to a triangle using the Geogebra tool.

You can either use the online version of Geogebra or you can download Geogebra Classic 5 or Geogebra Classic 6. Note that the screen shots shown below are based on Geogebra Classic 5, however Geogebra Classic 6 is very similar.

1. Open a new Geogebra window, ensuring that the grid and axes are shown.
   

2. Using the “Move Graphics View” tool, move the window so that the window is focussed on the 1st quadrant of the Cartesian plane.
   

   

3. Use the “Point” tool to create a point at the origin of the Cartesian plane (0,0). This is referred to as the enlargement origin.
   

4. Use the “Polygon” tool to create a triangle with all three vertices in the 1st quadrant.
   

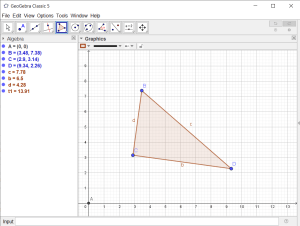
5. Use the “Line” tool to create three lines that each pass through the transformation origin and one of the vertices of the triangle.
   

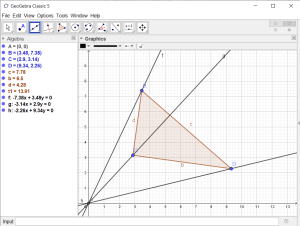
6. Use the “Enlarge from Point” tool to create a second triangle which is an enlargement of the first.
   1. Select the “Enlarge from Point” tool
      

   2. Click on the original triangle
   3. Select the enlargement origin
   4. Enter a scale factor of 2

   

7. Measure the three internal angles of the first triangle

   1. Select the “Angle” tool

      

   2. Click within the first triangle – all three angles should be
      marked.

8. Repeat the above steps to measure all three internal angles of
   the second triangle.

9. Record your measurements in a table like the one below:

   	Angle 1	Angle 2	Angle 3
   Triangle 1
   Triangle 2

10. Measure the three sides of the first triangle

    1. Select the “Distance or Length” tool

       

    2. Select the two vertices at either end of the side

    3. Repeat for the other two sides

11. Repeat the above steps for the second triangle.

12. Record your measurements in a table like the one below. Include
    calculations of the ratios between side lengths for each of the two
    triangles.

    	Side 1	Side 2	Side 3	Side 1 ÷ Side 2	Side 1 ÷ Side 3	Side 2 ÷ Side 3
    Triangle 1
    Triangle 2

13. Calculate the area of the first triangle using the “Area” tool

1. Select the “Area” tool

   

2. Click on the triangle

14. Repeat for the second triangle.

15. Insert your measurements of area in a table like the one
    below:

    	Area
    Triangle 1
    Triangle 2

16. Save your Geogebra file as “enlargement_transformation.ggb” using
    “Save” from the “File” menu.

17. Export your enlargement diagram to a “PNG” file using
    “Export”->”Graphics View” from the “File” menu.

18. With reference to your measurements in the three tables, comment
    on how the angles, side lengths, rations between sides, and area are
    affected by an enlargement transformation with a scale factor of
    2.

19. Predict what will happen to the angles, side lengths, ratios
    between sides, and area, if the original triangle is enlarged by a scale
    factor of 3.

20. Use Geogebra to test your prediction, include an exported image
    file as evidence.

21. Summarise your findings with four hypotheses relating to the
    angles, side lengths, ratios between sides, and area of enlarged
    triangles with a scale factor of n.